C# 전산수학 - 정적분을 통한 원주율 계산

여기서는 C#으로 원주율의 근사값을 계산하는 간단한 프로그램을 만들어 봅시다. 원주율을 계산하는 방법은 여러가지가 있습니다만, 이번 포스팅에서는 정적분을 이용해서 근사값을 구해보도록 하겠습니다.

아크탄젠트 함수의 도함수를 적분하는 방법을 사용하면, 원주율을 유리함수의 정적분으로 나타내는 것이 가능합니다.

\[ \begin{array}{l} \displaystyle \pi = 4 \left[ \arctan{(1)} - \arctan{(0)} \right] \\ \displaystyle \phantom{\pi} = 4 \int_0^1 du \left[ \frac{d}{du} \arctan{(u)} \right] \\ \displaystyle \phantom{\pi} = 4 \int_0^1 du \, \left( \frac{1}{1 + u^2} \right) \end{array} \]

먼저 적분대상이 되는 함수 (integrand)와 적분 구간을 매개변수로 받아서 정적분의 근사값을 구하는 함수를 작성하는것이 편리합니다. 여기서는 사다리꼴 공식을 통해 계산을 하게 될텐데요. 수학적인 원리와 C언어 프로그래밍을 이용한 예시는 다음 포스팅에 더 자세하게 소개되어 있습니다.

사다리꼴 공식을 이용한 C/C++ 수치 적분

C# 소스 코드입니다.
IntegralTrapezoidal.cs [다운로드]

using System;

namespace MathTools {

    class Integral {
        public static double get_trapezoidal(double xmin,
                                             double xmax,
                double eps_precision,
                Func<double, double> integrand) {
            double ret_now = 0.0;
            double ret_prev;
            bool converging = false;

            ulong nbin_x = 1;
            double delta_x =
                (xmax - xmin) / (double)nbin_x;

            int istep = 1;
            while (!converging) {
                ret_prev = ret_now;

                ulong ix;
                if (istep == 1) {
                    ret_now = 0.0;
                    for (ix = 0; ix < nbin_x; ix++) {
                        double x0 = xmin + delta_x * (double)ix;
                        double x1 = x0 + delta_x;
                        ret_now +=
                            0.5 * delta_x * (integrand(x0) +
                                             integrand(x1));
                    }
                } else {
                    ret_now = 0.5 * ret_prev;
                    for (ix = 0; ix <= nbin_x; ix++) {
                        if (ix % 2 == 0) {
                            continue;
                        }

                        double x_now = xmin + delta_x * (double)ix;
                        ret_now +=
                            delta_x * integrand(x_now);
                    }
                }

                Console.WriteLine("      step " + istep +
                                  " : integral = " + ret_now);
            
                if (Math.Abs(ret_now - ret_prev) <
                    0.5 * eps_precision *
                    Math.Abs(ret_now + ret_prev)) {
                    converging = true;
                }

                istep += 1;
                nbin_x = 2 * nbin_x;
                delta_x = 0.5 * delta_x;
            }

            return ret_now;
        }
    }
}

정적분의 근사값을 계산하는 Integral.get_trapezoidal이라는 함수는 적분의 범위와 정밀도 및 적분대상이 되는 함수를 매개변수로 받고 있습니다. 변수가 아닌 함수를 매개변수로 사용하기 위해 Func 대리자 (delegate)를 사용했습니다.

매개변수 eps_precision을 통해서 원하는 정밀도를 설정할 수 있는데요. 근사값을 구하기 위한 사다리꼴의 갯수를 2배로 늘렸을 때, 새로운 근사값이 기존 값에 비해 달라지는 비율이 eps_precision보다 작다면 수렴하는 것으로 가정하게 됩니다.

이제 특정한 함수를 적분하여 원주율을 구하기 위한 Main 프로그램을 만들어 봅시다. 앞에서 언급한 아크탄젠트 함수의 도함수를 적분하게 되는데, 여기서 적분 대상이 되는 함수의 이름은 func_integrand입니다. Main 함수에서는 func_integrand 함수를 매개변수로 해서 Integral.get_trapezoidal 함수를 호출하게 됩니다.

C# 소스 코드입니다.
test_calc_pi.cs [다운로드]

using System;
using MathTools;

namespace Calc_M_PI {
    class Program {
        static void Main(string[] args) {
            double val_pi =
                Integral.get_trapezoidal(0.0, 1.0, 1e-12,
                                         func_integrand);

            Console.WriteLine("");
            Console.WriteLine("pi from numerical integration");
            Console.WriteLine("  > pi = " + val_pi);
            Console.WriteLine("pi from C# math library");
            Console.WriteLine("  > pi = " + Math.PI);
        }

        static double func_integrand(double u) {
            return 4.0 / (1.0 + u * u);
        }
    }
}

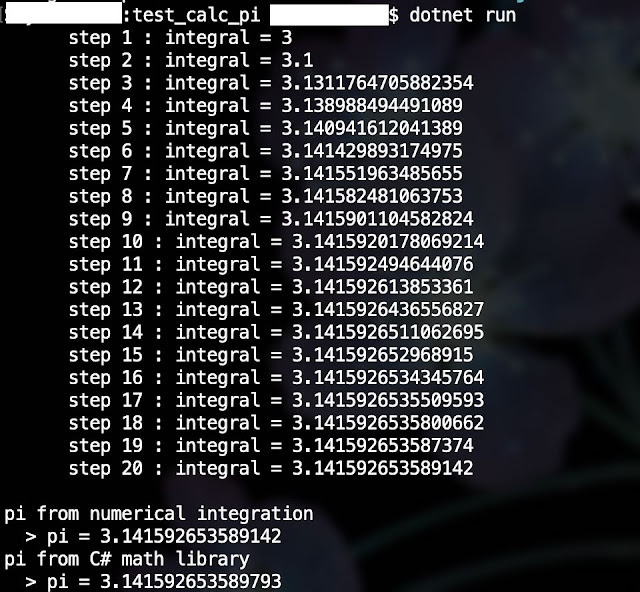
마이크로소프트 비주얼 스튜디오나 .NET Core를 통해 프로그램을 빌드할 수 있습니다.

프로그램을 실행하고 C# 수학 함수 라이브러리에 정의된 원주율 값과 비교해보면, 소수점 아래 12자리까지 일치하는 것을 볼 수 있습니다.

이번 포스팅에서는 C# 프로그램을 소개했습니다만, C언어나 C++에서도 비슷한 프로그램을 작성해 볼 수 있습니다. 다음 포스팅에 더 자세한 내용이 소개되어 있습니다.

C/C++ 원주율 계산 프로그램